वृत्त (Circles)
वृत्त (Circles)
वृत्त एक ऐसी ज्यामितीय आकृति है जिसमें सभी बिंदु केंद्र से समान दूरी पर होते हैं। यह कक्षा 10 में एक महत्वपूर्ण विषय है और इसे समझने के लिए कुछ मुख्य बिंदु और परिभाषाएँ निम्नलिखित हैं:
वृत्त की परिभाषा (Definition of a Circle)
वृत्त एक समतल में स्थित उन बिंदुओं का समुच्चय है जो एक नियत बिंदु (केंद्र) से समान दूरी पर होते हैं। इस निश्चित दूरी को त्रिज्या (Radius) कहते हैं और नियत बिंदु को केंद्र (Centre) कहते हैं।
मुख्य तत्व:
- केंद्र (Centre):
वह बिंदु जिससे समान दूरी पर सभी बिंदु होते हैं।
- त्रिज्या (Radius):
केंद्र से वृत्त की परिधि (boundary) तक की दूरी।
- व्यास (Diameter):
वह रेखाखंड जो वृत्त की परिधि को दो बिंदुओं पर छूता है और केंद्र से होकर गुजरता है। व्यास वृत्त का सबसे लंबा रेखा खंड है और यह त्रिज्या का दोगुना होता है। (D = 2r)
वृत्त से जुड़े महत्वपूर्ण शब्दावली (Key Terms Related to Circle)
i. परिधि (Circumference):
वृत्त की बाहरी सीमा, जिसे वृत्त का घेरा कहा जाता है।
ii. जीवा (Chord):
वृत्त की परिधि पर स्थित दो बिंदुओं को जोड़ने वाला रेखा खंड। सबसे लंबी जीवा व्यास होती है।
iii. खंड (Segment):
किसी वृत्त में एक जीवा के द्वारा बने दो भागों में से कोई एक भाग। जीवा वृत्त को दो खंडों में विभाजित करती है - एक छोटा खंड (minor segment) और एक बड़ा खंड (major segment)
iv. खंडाकार क्षेत्र (Sector):
केंद्र से निकली दो त्रिज्याओं द्वारा वृत्त के क्षेत्र को विभाजित करने वाला भाग।
v. स्पर्श रेखा (Tangent):
एक ऐसी रेखा जो वृत्त को केवल एक बिंदु पर स्पर्श करती है।
वृत्त की स्पर्श रेखा (Tangent of a Circle)
स्पर्श रेखा किसी वृत्त को केवल एक बिंदु पर छूने वाली रेखा होती है। इसे "Touching Line" भी कहा जाता है। यह हमेशा वृत्त की त्रिज्या पर लंबवत होती है।
स्पर्श रेखा की विशेषताएँ (Properties of Tangent):
i. किसी भी वृत्त से एक बिंदु पर खींची गई स्पर्श रेखा त्रिज्या पर लंबवत होती है।
ii. किसी बिंदु से केवल एक स्पर्श रेखा खींची जा सकती है।
iii. यदि वृत्त के बाहर के किसी बिंदु से वृत्त को दो स्पर्श रेखाएँ खींची जाती हैं, तो वे स्पर्श रेखाएँ समान लंबाई की होती हैं।
वृत्त पर आधारित प्रश्नों का हल (Example Problems)
Example 1 (उदाहरण 1):
एक वृत्त का व्यास (10 , cm) है। वृत्त की त्रिज्या ज्ञात करें।
Example 2 (उदाहरण 2):
वृत्त का केंद्र O है। किसी बिंदु P से एक स्पर्श रेखा खींची गई है, जिसका वृत्त के केंद्र तक की दूरी 12 cm है और त्रिज्या 5 cm है। स्पर्श रेखा PQ की लंबाई ज्ञात करें।
Solution (हल):
यह त्रिकोण OPQ एक समकोण त्रिकोण है, क्योंकि स्पर्श रेखा त्रिज्या पर लंबवत होती है।
इसलिए, हम पायथागोरस प्रमेय का उपयोग कर सकते हैं:
OP2 = OQ2 + PQ2
जहाँ,
OP = 12 cm और OQ = 5 cm
122 = 52 + PQ2
144 = 25 + PQ2
PQ2 = 144 - 25
PQ2 = 119
PQ = √119
PQ = approx 10.9 cm
वृत्तों के उपयोग (Applications of Circles)
i. यातायात के साइन बोर्ड
ii. गोलाकार वस्तुएँ जैसे बॉल, घड़ियाँ, आदि
iii. यांत्रिकी में चक्के और गियर
वृत्त के इन तत्वों का जीवन में बहुत महत्व है और यह ज्यामिति के साथ-साथ विज्ञान, इंजीनियरिंग और रोजमर्रा की समस्याओं को हल करने में मदद करता है।
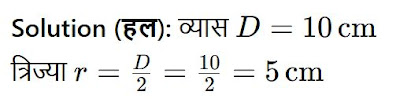
टिप्पणियाँ
एक टिप्पणी भेजें