दो चरों वाले रैखिक समीकरण (Pair of Linear Equations in Two Variables)
रैखिक समीकरण युग्म (Pair of Linear Equations in Two Variables)
परिभाषा:
दो चरों वाले रैखिक समीकरण का मतलब है ऐसे समीकरण जिनमें दो चर होते हैं और प्रत्येक चर का घात (power) 1 होता है। जब दो ऐसे रैखिक समीकरणों को एक साथ हल किया जाता है, तो इसे "दो चरों वाले रैखिक समीकरणों का युग्म" (Pair of Linear Equations in Two Variables) कहा जाता है।
सामान्य रूप:
[a1x + b1y + c1 = 0]
[a2x + b2y + c2 = 0]
जहाँ (a1, b1, c1, a2, b2, c2) वास्तविक संख्याएँ हैं और (x) और (y) दो चर (variables) हैं।
नोट: (a1) और (b1) एक साथ शून्य नहीं हो सकते; इसी प्रकार (a2) और (b2) भी शून्य नहीं हो सकते।
हल करने के तरीके (Methods to Solve Pair of Linear Equations)
1. प्रतिस्थापन विधि (Substitution Method):
- एक समीकरण से किसी एक चर का मान ज्ञात करें और उसे दूसरे समीकरण में प्रतिस्थापित करें।
- प्राप्त सरल समीकरण को हल करें और एक चर का मान प्राप्त करें।
- इसे पहले समीकरण में रखकर दूसरे चर का मान निकालें।
2. उपलेखन विधि (Elimination Method):
- दोनों समीकरणों में से एक चर के गुणांक को बराबर करें।
- जोड़ने या घटाने की क्रिया द्वारा एक चर को समाप्त करें और दूसरे चर का मान ज्ञात करें।
- ज्ञात मान को किसी एक समीकरण में रखकर दूसरे चर का मान प्राप्त करें।
3. क्रॉस गुणन विधि (Cross Multiplication Method):
- इस विधि में समीकरणों को इस रूप में हल किया जाता है:
.JPG "क्रॉस गुणन विधि (Cross Multiplication Method)")
- यह विधि तब उपयोगी होती है जब समीकरण को सटीक रूप से हल करना होता है।
4. ग्राफिक विधि (Graphical Method):
- दोनों समीकरणों का ग्राफ बनाएं और उनकी रेखाओं को खींचें।
- जहाँ दोनों रेखाएँ एक दूसरे को काटती हैं, वह बिंदु दोनों समीकरणों का हल होता है।
हल करने का उदाहरण (Example)
समीकरण:
2x + 3y = 8
4x - y = -2
प्रतिस्थापन विधि से हल करना:
Step1. पहले समीकरण से (y) का मान ज्ञात करें:
Step2. इस मान को दूसरे समीकरण में प्रतिस्थापित करें:
Step3. समीकरण को हल करें:
Step4. (x) का मान ज्ञात होने पर इसे पहले समीकरण में रखें और (y) का मान निकालें:
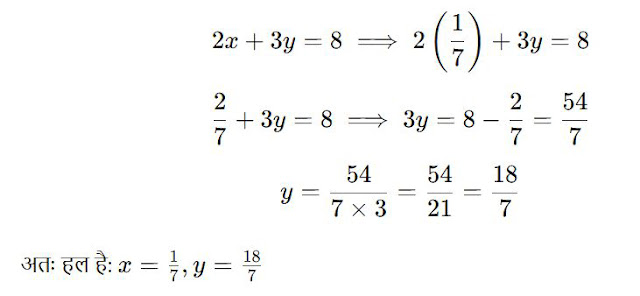
अलग-अलग हल के परिणाम (Types of Solutions)
i. संगत और अद्वितीय हल (Consistent and Unique Solution):
- रेखाएँ एक बिंदु पर मिलती हैं।
ii. संगत और अनंत हल (Consistent and Infinitely Many Solutions):
- रेखाएँ एक ही लाइन हैं (अर्थात् वे मिलती हुई रेखाएँ हैं)।
iii. असंगत हल (Inconsistent Solution):
- रेखाएँ समांतर होती हैं और कभी नहीं मिलतीं।
यदि आपको कोई और उदाहरण या किसी विशेष विधि पर विस्तार से जानकारी चाहिए, तो कृपया कमेण्त करके हमें जरुर बताएं!
टिप्पणियाँ
एक टिप्पणी भेजें